# Nibiru
Nibiru is a breakthrough L1 blockchain and smart contract ecosystem providing superior throughput and unparalleled security. Nibiru aims to be the most developer-friendly and user-friendly smart contract platform in Web3.
Build on Nibiru
From smart contract guides to essential Web3 primitives and infrastructure, utilize Nibiru's developer friendly SDKs to build decentralized applications.
Use Nibiru Chain
Kickstart your journey as a user of Nibiru. Learn how to create wallets, stake NIBI, participate in campaigns, or use the Nibiru web application.
Learn Core Concepts
Build an understanding of the core concepts behind how Nibiru Chain works. Topics explored in this section provide a solid foundation on both the Nibiru blockchain and Web3 in general.
Join the Community
Engage with the Nibiru community, a global community of software developers, content creators, node runners, and Web3 enthusiasts.
# For Users
Engage with Nibiru's fast-growing community or get started by accessing a wealth of resources and tutorials below.
- Nibiru Community Hub
- Nibiru Web App (opens new window)
- Guide: Set Up a Nibiru Chain Wallet
- Guide: Staking on Nibiru
# For Devs
- Smart Contract Sandbox (NibiruChain/nibiru-wasm) (opens new window)
- TypeScript SDK: NibiJS
- Rust SDK:
nibiru_std(opens new window) - Golang SDK: Gonibi
- Python SDK
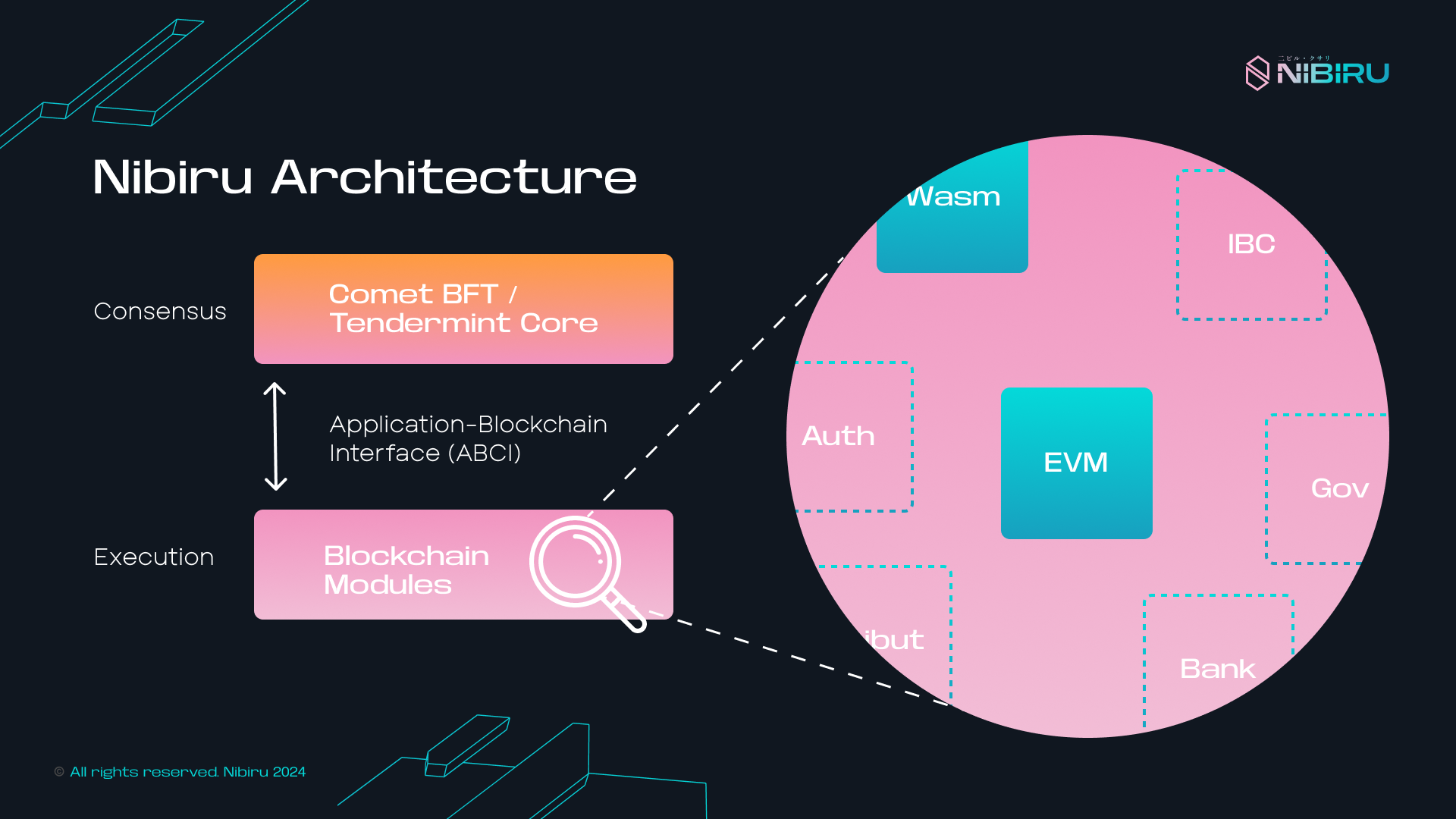
# Learn About Nibiru
Nibiru acts as a permission-less platform for developers to deploy secure, production-grade smart contracts.
NibiruBFT: Consenus Engine
Instant finality, consistent security, and Byzantine Fault Tolerant state machine replication.
Frequently Asked Questions (FAQ)
Kickstart your journey as a user of Nibiru. Learn how to create wallets, stake NIBI, participate in campaigns, or use the Nibiru web application.
Nibiru Wasm
WebAssembly (Wasm) smart contract execution environment programmed in Rust.
Nibiru Roadmap (2025)
A brief sneak peek at onging and upcoming improvements to Nibiru.
Tokenomics
Understand NIBI, the staking and utility token of Nibiru Chain that powers the network's consensus engine, governance, and computation as "gas".
Guide: Building with NibiJS
A brief guide on Nibiru's APIs, docs, and resources to broadcast transactions and query the chain.
# Nibiru Ecosystem: Featured Apps
Explore a more comprehensive set of projects building on Nibiru in our Ecosystem Hub (opens new window).
Sai.fun Perps Exchange: A perpetual futures exchange where users can take leveraged exposure and trade on a plethora of assets — completely on-chain, completely non-custodially, and with minimal gas fees.
Astrovault (opens new window): A unique exchange prioritizing efficiency, low-friction trading, and rewards.
Nibiru Oracle: Nibiru accurately prices assets using a native, system of decentralized oracles. Both external APIs and smart contracts can tap into the Oracle Module for secure, low-latency feeds.
# Contribution Guidelines
You can contribute to improve this documentation by submitting a
GitHub ticket in our website-help repository (opens new window).